A cylinder of radius r is surmounted on a hemisphere of same radius. If total height of the object is 13 cm, then its inner surface area is

A cylinder of radius r is surmounted on a hemisphere of same radius. If total height of the object is 13 cm, then its inner surface area is :

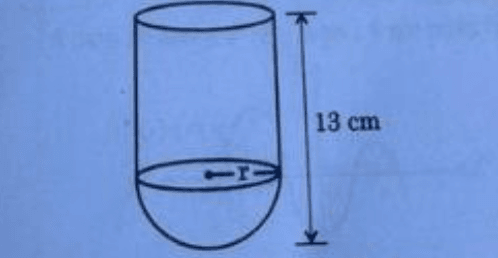
(Α) 2πr(r +13)
(Β) 13πг
(C) 2(13+r)2
(D) 26πr

Solution : Correct answer is : (D) 26πr.

We’re given:

• A cylinder of radius = r
• A hemisphere of the same radius r placed on top
• Total height of the object = 13 cm

Height of cylinder = ?
Height of hemisphere = r

So,

Total height = height of cylinder + height of hemisphere$$13 = h + r$$

So,$$h = 13 – r$$Inner surface area includes:

1. Curved surface area of cylinder
2. Curved surface area of hemisphere

(No base area included because we are talking about inner surface only.)

Curved surface area of cylinder:$$2\pi r h$$

Substitute $h = 13 – r$h=13−r:$$2\pi r (13 – r)$$

Curved surface area of hemisphere:$$2\pi r^2$$Add both areas

$$2\pi r (13 – r) + 2\pi r^2$$2πr(13−r)+2πr2

Factor out $2\pi r$2πr:$$2\pi r (13 – r + r)$$$$= 2\pi r (13)$$$$= 26\pi r$$

Final Answer:

$$\boxed{26\pi r}$$

(D) 26πr